A Puzzle Equivalent to Factoring a Quadratic

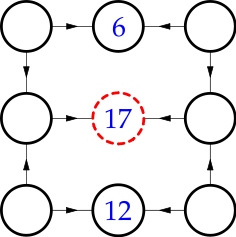
In response to The Number Warrior’s post, I would like to propose an alternative, since the choice to do the sum or product inheres more to the nodes than the connections.  In the following, the style of line tells you what to do with the numbers from the lines coming into the node:

• solid black = multiply the incoming numbers (so that the node is the product)
• dashed red = add the incoming numbers (so that the node is the sum)

A puzzle equivalent to factoring a quadratic

factorpuzzle (PDF)

N.B.: I did this more as an exercise in using Asymptote (and its flowchart package) than to make any real contribution.  For the interested, here is the source code:

size(6cm,0);
import flowchart;
// for lines coming into a node, solid lines mean multiply, dashed lines mean add

int a = 6;
int b = 17;
int c = 12;

real step = .2;
real radius = 18;
pen number = blue+linewidth(2)+fontsize(20pt)+Palatino();
pen sum = red+linetype("2 2")+linewidth(2);
pen product = black+linewidth(2);
pen connection = black+linewidth(2);

block A=circle(Label(string(a),number),(0,step),drawpen=product,mindiameter=2*radius);
block B=circle(Label(string(b),number),(0,0),drawpen=sum,mindiameter=2*radius);
block C=circle(Label(string(c),number),(0,-step),drawpen=product,mindiameter=2*radius);

block d1=circle("",(-step,step),drawpen=product,mindiameter=2*radius);
block d2=circle("",(step,step),drawpen=product,mindiameter=2*radius);
block e2=circle("",(-step,-step),drawpen=product,mindiameter=2*radius);
block e1=circle("",(step,-step),drawpen=product,mindiameter=2*radius);
block cross12=circle("",(-step,0),drawpen=product,mindiameter=2*radius);
block cross21=circle("",(step,0),drawpen=product,mindiameter=2*radius);

add(new void(picture pic, transform t) {
    draw(pic,path(new pair[]{d1.right(t),A.left(t)}),MidArrow);
    draw(pic,path(new pair[]{d2.left(t),A.right(t)}),MidArrow);
    draw(pic,path(new pair[]{e2.right(t),C.left(t)}),MidArrow);
    draw(pic,path(new pair[]{e1.left(t),C.right(t)}),MidArrow);
    draw(pic,path(new pair[]{cross12.right(t),B.left(t)}),MidArrow);
    draw(pic,path(new pair[]{cross21.left(t),B.right(t)}),MidArrow);
    draw(pic,path(new pair[]{d1.bottom(t),cross12.top(t)}),MidArrow);
    draw(pic,path(new pair[]{e2.top(t),cross12.bottom(t)}),MidArrow);
    draw(pic,path(new pair[]{d2.bottom(t),cross21.top(t)}),MidArrow);
    draw(pic,path(new pair[]{e1.top(t),cross21.bottom(t)}),MidArrow);
  });

draw(A);
draw(B);
draw(C);
draw(d1);
draw(d2);
draw(e1);
draw(e2);
draw(cross12);
draw(cross21);